9608. Такси

Ивана и Сергея пригласили принять участие в областной олимпиаде по информатике.

Поскольку они живут в разных населённых пунктах, Иван предложил воспользоваться услугами такси, чтобы добраться до места проведения олимпиады.

Такси выезжает из пункта A, где живёт Иван, направляется в пункт B, чтобы забрать Сергея, а затем едет в пункт C, где проходит олимпиада.

Зная расстояния между населёнными пунктами и стоимость одного километра поездки на такси, определите, на сколько больше придётся заплатить, если заехать за Сергеем, чем ехать напрямую к месту проведения олимпиады. Предполагается, что такси всегда выбирает кратчайший из возможных маршрутов.

Вход. В первой строке даны пять чисел: четыре целых и одно вещественное:

· n – количество населенных пунктов,

· A – номер населённого пункта, где живёт Иван,

· B – номер населённого пункта, где живёт Сергей,

· С – номер населённого пункта, где проходит олимпиада,

· d – стоимость проезда одного километра на такси. 

Во второй строке задано целое число m – количество дорог.

Далее следуют m строк, каждая из которых описывает одну дорогу: два целых числа – номера населённых пунктов, которые она соединяет, и одно вещественное число – длина этой дороги в километрах.

Все номера населённых пунктов – натуральные числа, не превышающие 100.

Выход. Выведите одно вещественное число – сумму, на которую дороже обошлась поездка с заездом за Сергеем по сравнению с прямым маршрутом.

Если маршрута из пункта A до пункта B или из пункта A до пункта C не существует, выведите -1.

Пример входа	Пример выхода
5 1 2 3 4.25 5 1 4 2.5 4 2 3 4 5 3 3 5 2 3 4 8	25.5

РЕШЕНИЕ

графы - Дейкстра

Анализ алгоритма

Во взвешенном графе с помощью алгоритма Дейкстры определяются:

· кратчайшее расстояние dist_ab от пункта A до пункта B;

· кратчайшее расстояние dist_ac от пункта A до пункта C;

· кратчайшее расстояние dist_bc от пункта B до пункта C;

Без заезда за Сергеем Иван проезжает расстояние dist_ac.

С заездом за Сергеем он проезжает путь длиной dist_ab + dist_bc.

Ответ на задачу равен

(dist_ab + dist_bc – dist_ac) * d

Это сумма, на которую поездка стала дороже из-за заезда за Сергеем.

Пример

Граф дорог имеет следующий вид:

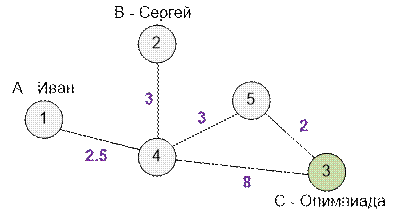
Вычислим кратчайшие расстояния:

· кратчайший путь dist_ab от A до B равен 5.5;

· кратчайший путь dist_ac от A до C равен 7.5;

· кратчайший путь dist_bc от B до C равен 8;

Расстояние, которое проезжает Иван без заезда за Сергеем: dist_ac = 7.5.

Расстояние с заездом за Сергеем: dist_ab + dist_bc = 5.5 + 8 = 13.5.

Тогда ответ на задачу равен:

(dist_ab + dist_bc – dist_ac) * d = (5.5 + 8 – 7.5) * 4.25 = 6 * 4.25 = 25.5

Реализация алгоритма

Граф храним в виде взвешенной матрицы смежности g. Объявим массив кратчайших расстояний dist и массив used, содержащий информацию о вершинах, для которых расстояние уже вычислено.

#define MAX 110

double g[MAX][MAX], dist[MAX];

int used[MAX];

Функция Dijkstra возвращает длину кратчайшего пути от вершины s до вершины f.

double Dijkstra(int s, int f)

{

memset(used, 0, sizeof(used));

for (i = 1; i <= n; i++) dist[i] = 1e18;

dist[s] = 0;

for (i = 1; i < n; i++)

{

double min = 1e18;

int w = -1;

for (j = 1; j <= n; j++)

if (used[j] == 0 && dist[j] < min) { min = dist[j]; w = j; }

if (min == 1e18) break;

for (j = 1; j <= n; j++)

if (used[j] == 0) dist[j] = minimum(dist[j], dist[w] + g[w][j]);

used[w] = 1;

}

return dist[f];

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d %d %lf", &n, &a, &b, &c, &d);

scanf("%d", &m);

for (i = 1; i <= n; i++)

for (j = 1; j <= n; j++) g[i][j] = 1e18;

for (i = 0; i < m; i++)

{

scanf("%d %d %lf", &s, &f, &w);

g[s][f] = g[f][s] = w;

}

Вычисляем значения dist_ab, dist_bc, dist_ac.

double d1 = Dijkstra(a, b);

double d2 = Dijkstra(b, c);

double ds = Dijkstra(a, c);

Если хотя бы одно из этих значений равно бесконечности, значит, соответствующего маршрута не существует – в этом случае выводим -1.

if (d1 == 1e18 || d2 == 1e18 || ds == 1e18) printf("-1\n");

Иначе выводим ответ (dist_ab + dist_bc – dist_ac) * d.

else printf("%lf\n", (d1 + d2 - ds) * d);